Построение графиков функций — одна из возможностей  Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.

Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.

1) Рассмотрим пример построения графика линейной функции: y=5x-2

Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку

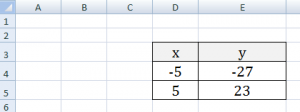
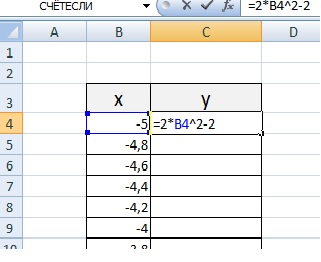
В нашем случае  y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.

В итоге мы получим табличку:

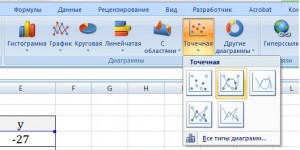
Теперь можно приступать к созданию графика.

Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)

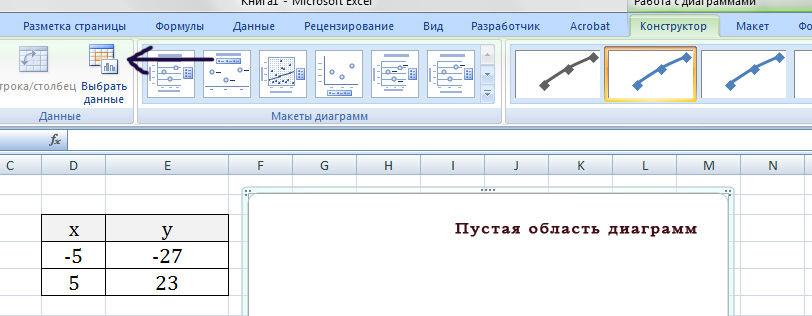
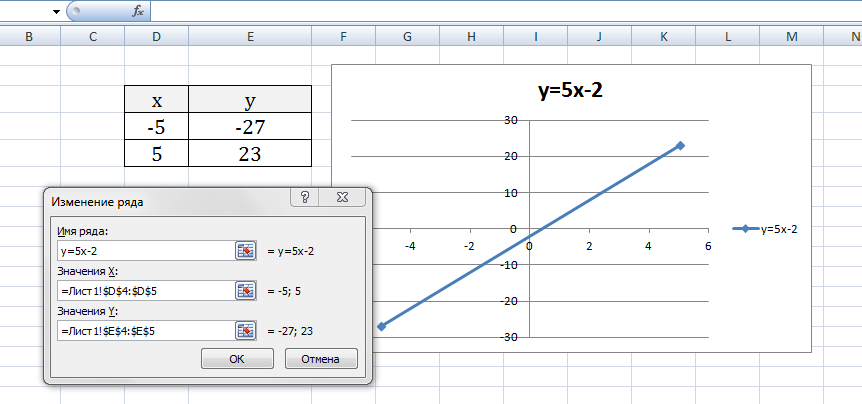
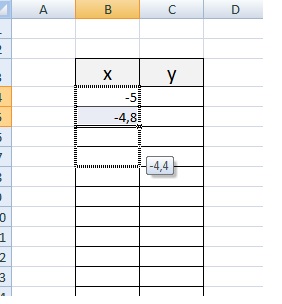
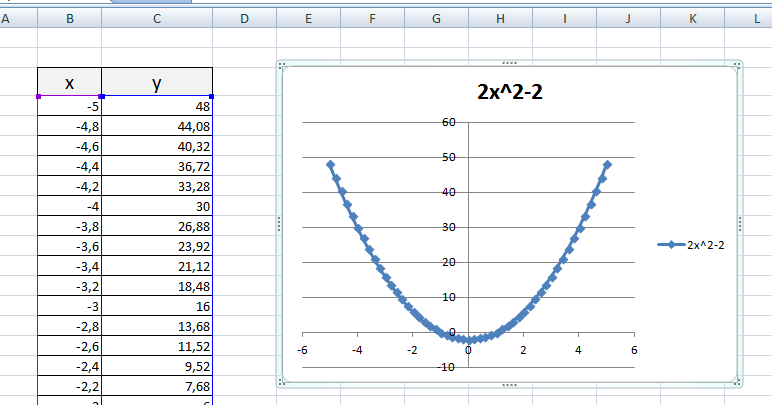
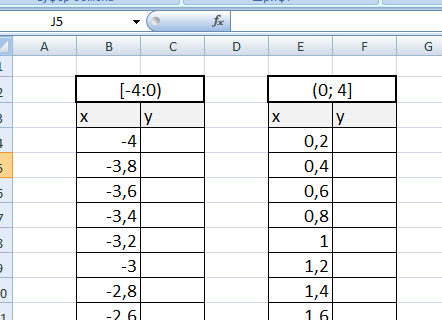
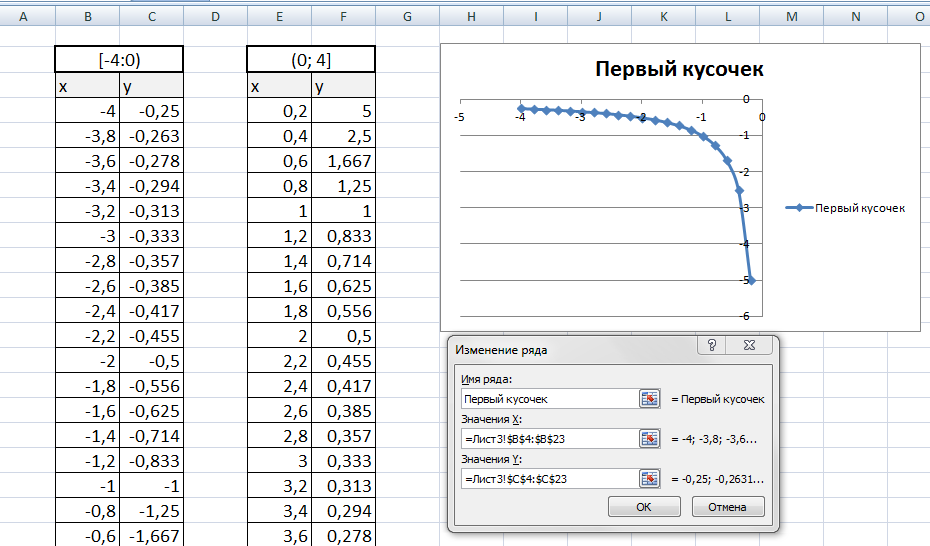
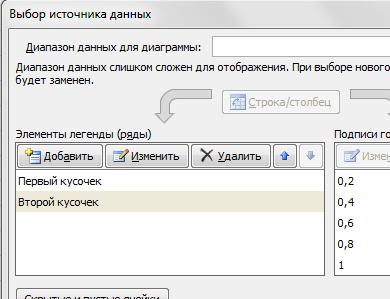
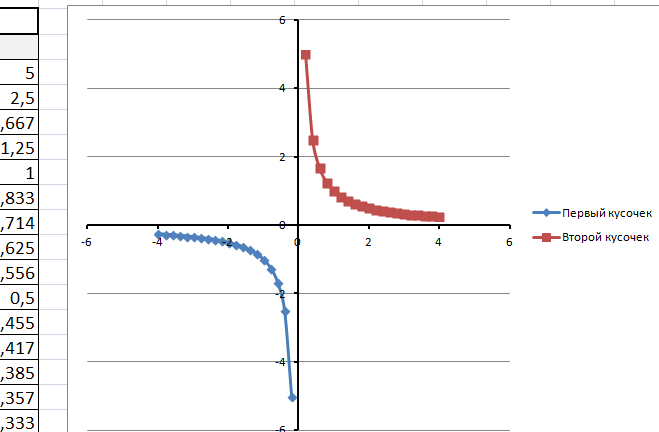
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ

 Выберем данные:  диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:

Нажимаем ОК. Перед нами график линейной функции.

2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2x²-2

Параболу по двум точкам уже не построить, в отличии от прямой.

Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу [-5; 5].

Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу 0,2.

Заполняю столбец со значениями х, используя маркер автозаполнения  до значения х=5.

Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.

Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.

Получим:

Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.

Любые другие графики непрерывных функций строятся аналогично.

3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.

Рассмотрим это на примере функции у=1/х.

Функция определена на интервалах (- беск;0) и (0; +беск)

Создадим график функции на интервалах: [-4;0) и (0; 4].

Подготовим две таблички, где х изменяется с шагом 0,2:

Находим значения функции от каждого аргумента х аналогично примерам выше.

На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно

Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА  значениями из второй таблички

Получаем график функции y=1/x

Спасибо за внимание!